K-means & 階層的クラスタリング#
# 表形式のデータを操作するためのライブラリ
import pandas as pd
# 機械学習用ライブラリsklearnのKmeansクラス
from sklearn.cluster import KMeans
# 距離行列の計算のためのライブラリ
import scipy.spatial.distance as distance
# 階層的クラスタリング用のライブラリ
from scipy.cluster.hierarchy import dendrogram, linkage, cut_tree
# グラフ描画ライブラリ
import matplotlib.pyplot as plt
import seaborn as sns;
sns.set(style='ticks')
%matplotlib inline
# 警告文を表示させないおまじない
import warnings
warnings.filterwarnings('ignore')
クイズ#
Q1: ユークリッド距離とコサイン類似度#
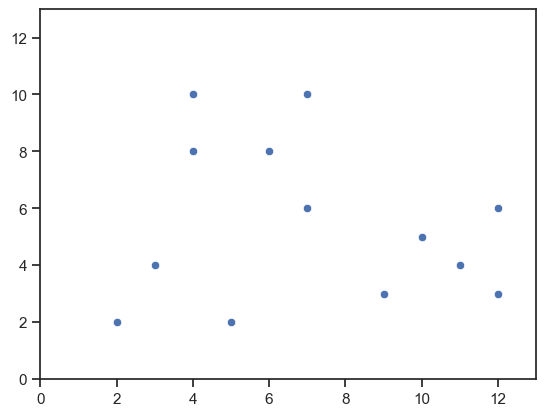
以下の図のように,2次元のユークリッド空間上に,13個のデータ点が図のように分布している状況を考える(各点の座標については,下記コードのリストdataに収められている).
N次元空間上の任意の点\(v_1\),\(v_2\)が与えられたとき,\(v_1\)と\(v_2\)のユークリッド距離を求める関数calc_euclidean_dist(v1, v2),コサイン類似度を求める関数calc_cosine_sim(v1, v2)を実装しなさい.
さらに,下図の13つの点のすべての組み合わせについて,そのユークリッド距離とコサイン類似度を求めなさい.
なお,実装する関数の第1引数および第2引数は,実数のリストを想定しなさい.
data = [(2, 2), (3, 4), (5, 2), (10, 5), (9, 3),
(11, 4), (12, 3), (12, 6), (4, 10), (4, 8),
(6, 8), (7, 10), (7, 6)]
xs, ys = zip(*data) # zipの逆操作
# 可視化
ax = sns.scatterplot(x=xs, y=ys)
ax.set_xlim(0, 13)
ax.set_ylim(0, 13)
plt.show()
# write your code
import math
def calc_euclidean_dist(v1, v2):
if len(v1) == len(v2):
dist = 0
for idx in range(len(v1)):
x1 = v1[idx]
x2 = v2[idx]
dist += (x1 - x2) ** 2
return math.sqrt(dist)
else:
return None
# write your code
# 内積
def inner_product(v1, v2):
if len(v1) == len(v2):
result = 0
for idx in range(len(v1)):
x1 = v1[idx]
x2 = v2[idx]
result += x1 * x2
return result
else:
return None
# ベクトルの絶対値
def norm(v):
result = 0
for x in v:
result += x ** 2
return math.sqrt(result)
def calc_cosine_sim(v1, v2):
if norm(v1) > 0 and norm(v2):
return inner_product(v1, v2) / (norm(v1) * norm(v2))
else:
return None
# データ数
N = len(data)
# ユークリッド距離
for i in range(N):
for j in range(i, N):
euclidean_dist = calc_euclidean_dist(data[i], data[j])
print(f'{data[i]} - {data[j]}: Euclidean = {euclidean_dist:.3f}')
(2, 2) - (2, 2): Euclidean = 0.000
(2, 2) - (3, 4): Euclidean = 2.236
(2, 2) - (5, 2): Euclidean = 3.000
(2, 2) - (10, 5): Euclidean = 8.544
(2, 2) - (9, 3): Euclidean = 7.071
(2, 2) - (11, 4): Euclidean = 9.220
(2, 2) - (12, 3): Euclidean = 10.050
(2, 2) - (12, 6): Euclidean = 10.770
(2, 2) - (4, 10): Euclidean = 8.246
(2, 2) - (4, 8): Euclidean = 6.325
(2, 2) - (6, 8): Euclidean = 7.211
(2, 2) - (7, 10): Euclidean = 9.434
(2, 2) - (7, 6): Euclidean = 6.403
(3, 4) - (3, 4): Euclidean = 0.000
(3, 4) - (5, 2): Euclidean = 2.828
(3, 4) - (10, 5): Euclidean = 7.071
(3, 4) - (9, 3): Euclidean = 6.083
(3, 4) - (11, 4): Euclidean = 8.000
(3, 4) - (12, 3): Euclidean = 9.055
(3, 4) - (12, 6): Euclidean = 9.220
(3, 4) - (4, 10): Euclidean = 6.083
(3, 4) - (4, 8): Euclidean = 4.123
(3, 4) - (6, 8): Euclidean = 5.000
(3, 4) - (7, 10): Euclidean = 7.211
(3, 4) - (7, 6): Euclidean = 4.472
(5, 2) - (5, 2): Euclidean = 0.000
(5, 2) - (10, 5): Euclidean = 5.831
(5, 2) - (9, 3): Euclidean = 4.123
(5, 2) - (11, 4): Euclidean = 6.325
(5, 2) - (12, 3): Euclidean = 7.071
(5, 2) - (12, 6): Euclidean = 8.062
(5, 2) - (4, 10): Euclidean = 8.062
(5, 2) - (4, 8): Euclidean = 6.083
(5, 2) - (6, 8): Euclidean = 6.083
(5, 2) - (7, 10): Euclidean = 8.246
(5, 2) - (7, 6): Euclidean = 4.472
(10, 5) - (10, 5): Euclidean = 0.000
(10, 5) - (9, 3): Euclidean = 2.236
(10, 5) - (11, 4): Euclidean = 1.414
(10, 5) - (12, 3): Euclidean = 2.828
(10, 5) - (12, 6): Euclidean = 2.236
(10, 5) - (4, 10): Euclidean = 7.810
(10, 5) - (4, 8): Euclidean = 6.708
(10, 5) - (6, 8): Euclidean = 5.000
(10, 5) - (7, 10): Euclidean = 5.831
(10, 5) - (7, 6): Euclidean = 3.162
(9, 3) - (9, 3): Euclidean = 0.000
(9, 3) - (11, 4): Euclidean = 2.236
(9, 3) - (12, 3): Euclidean = 3.000
(9, 3) - (12, 6): Euclidean = 4.243
(9, 3) - (4, 10): Euclidean = 8.602
(9, 3) - (4, 8): Euclidean = 7.071
(9, 3) - (6, 8): Euclidean = 5.831
(9, 3) - (7, 10): Euclidean = 7.280
(9, 3) - (7, 6): Euclidean = 3.606
(11, 4) - (11, 4): Euclidean = 0.000
(11, 4) - (12, 3): Euclidean = 1.414
(11, 4) - (12, 6): Euclidean = 2.236
(11, 4) - (4, 10): Euclidean = 9.220
(11, 4) - (4, 8): Euclidean = 8.062
(11, 4) - (6, 8): Euclidean = 6.403
(11, 4) - (7, 10): Euclidean = 7.211
(11, 4) - (7, 6): Euclidean = 4.472
(12, 3) - (12, 3): Euclidean = 0.000
(12, 3) - (12, 6): Euclidean = 3.000
(12, 3) - (4, 10): Euclidean = 10.630
(12, 3) - (4, 8): Euclidean = 9.434
(12, 3) - (6, 8): Euclidean = 7.810
(12, 3) - (7, 10): Euclidean = 8.602
(12, 3) - (7, 6): Euclidean = 5.831
(12, 6) - (12, 6): Euclidean = 0.000
(12, 6) - (4, 10): Euclidean = 8.944
(12, 6) - (4, 8): Euclidean = 8.246
(12, 6) - (6, 8): Euclidean = 6.325
(12, 6) - (7, 10): Euclidean = 6.403
(12, 6) - (7, 6): Euclidean = 5.000
(4, 10) - (4, 10): Euclidean = 0.000
(4, 10) - (4, 8): Euclidean = 2.000
(4, 10) - (6, 8): Euclidean = 2.828
(4, 10) - (7, 10): Euclidean = 3.000
(4, 10) - (7, 6): Euclidean = 5.000
(4, 8) - (4, 8): Euclidean = 0.000
(4, 8) - (6, 8): Euclidean = 2.000
(4, 8) - (7, 10): Euclidean = 3.606
(4, 8) - (7, 6): Euclidean = 3.606
(6, 8) - (6, 8): Euclidean = 0.000
(6, 8) - (7, 10): Euclidean = 2.236
(6, 8) - (7, 6): Euclidean = 2.236
(7, 10) - (7, 10): Euclidean = 0.000
(7, 10) - (7, 6): Euclidean = 4.000
(7, 6) - (7, 6): Euclidean = 0.000
# コサイン類似度
for i in range(N):
for j in range(i, N):
cosine_sim = calc_cosine_sim(data[i], data[j])
print(f'{data[i]} - {data[j]}: Cosine = {cosine_sim:.3f}')
(2, 2) - (2, 2): Cosine = 1.000
(2, 2) - (3, 4): Cosine = 0.990
(2, 2) - (5, 2): Cosine = 0.919
(2, 2) - (10, 5): Cosine = 0.949
(2, 2) - (9, 3): Cosine = 0.894
(2, 2) - (11, 4): Cosine = 0.906
(2, 2) - (12, 3): Cosine = 0.857
(2, 2) - (12, 6): Cosine = 0.949
(2, 2) - (4, 10): Cosine = 0.919
(2, 2) - (4, 8): Cosine = 0.949
(2, 2) - (6, 8): Cosine = 0.990
(2, 2) - (7, 10): Cosine = 0.985
(2, 2) - (7, 6): Cosine = 0.997
(3, 4) - (3, 4): Cosine = 1.000
(3, 4) - (5, 2): Cosine = 0.854
(3, 4) - (10, 5): Cosine = 0.894
(3, 4) - (9, 3): Cosine = 0.822
(3, 4) - (11, 4): Cosine = 0.837
(3, 4) - (12, 3): Cosine = 0.776
(3, 4) - (12, 6): Cosine = 0.894
(3, 4) - (4, 10): Cosine = 0.966
(3, 4) - (4, 8): Cosine = 0.984
(3, 4) - (6, 8): Cosine = 1.000
(3, 4) - (7, 10): Cosine = 0.999
(3, 4) - (7, 6): Cosine = 0.976
(5, 2) - (5, 2): Cosine = 1.000
(5, 2) - (10, 5): Cosine = 0.997
(5, 2) - (9, 3): Cosine = 0.998
(5, 2) - (11, 4): Cosine = 0.999
(5, 2) - (12, 3): Cosine = 0.991
(5, 2) - (12, 6): Cosine = 0.997
(5, 2) - (4, 10): Cosine = 0.690
(5, 2) - (4, 8): Cosine = 0.747
(5, 2) - (6, 8): Cosine = 0.854
(5, 2) - (7, 10): Cosine = 0.837
(5, 2) - (7, 6): Cosine = 0.947
(10, 5) - (10, 5): Cosine = 1.000
(10, 5) - (9, 3): Cosine = 0.990
(10, 5) - (11, 4): Cosine = 0.993
(10, 5) - (12, 3): Cosine = 0.976
(10, 5) - (12, 6): Cosine = 1.000
(10, 5) - (4, 10): Cosine = 0.747
(10, 5) - (4, 8): Cosine = 0.800
(10, 5) - (6, 8): Cosine = 0.894
(10, 5) - (7, 10): Cosine = 0.879
(10, 5) - (7, 6): Cosine = 0.970
(9, 3) - (9, 3): Cosine = 1.000
(9, 3) - (11, 4): Cosine = 1.000
(9, 3) - (12, 3): Cosine = 0.997
(9, 3) - (12, 6): Cosine = 0.990
(9, 3) - (4, 10): Cosine = 0.646
(9, 3) - (4, 8): Cosine = 0.707
(9, 3) - (6, 8): Cosine = 0.822
(9, 3) - (7, 10): Cosine = 0.803
(9, 3) - (7, 6): Cosine = 0.926
(11, 4) - (11, 4): Cosine = 1.000
(11, 4) - (12, 3): Cosine = 0.995
(11, 4) - (12, 6): Cosine = 0.993
(11, 4) - (4, 10): Cosine = 0.666
(11, 4) - (4, 8): Cosine = 0.726
(11, 4) - (6, 8): Cosine = 0.837
(11, 4) - (7, 10): Cosine = 0.819
(11, 4) - (7, 6): Cosine = 0.936
(12, 3) - (12, 3): Cosine = 1.000
(12, 3) - (12, 6): Cosine = 0.976
(12, 3) - (4, 10): Cosine = 0.585
(12, 3) - (4, 8): Cosine = 0.651
(12, 3) - (6, 8): Cosine = 0.776
(12, 3) - (7, 10): Cosine = 0.755
(12, 3) - (7, 6): Cosine = 0.894
(12, 6) - (12, 6): Cosine = 1.000
(12, 6) - (4, 10): Cosine = 0.747
(12, 6) - (4, 8): Cosine = 0.800
(12, 6) - (6, 8): Cosine = 0.894
(12, 6) - (7, 10): Cosine = 0.879
(12, 6) - (7, 6): Cosine = 0.970
(4, 10) - (4, 10): Cosine = 1.000
(4, 10) - (4, 8): Cosine = 0.997
(4, 10) - (6, 8): Cosine = 0.966
(4, 10) - (7, 10): Cosine = 0.974
(4, 10) - (7, 6): Cosine = 0.886
(4, 8) - (4, 8): Cosine = 1.000
(4, 8) - (6, 8): Cosine = 0.984
(4, 8) - (7, 10): Cosine = 0.989
(4, 8) - (7, 6): Cosine = 0.922
(6, 8) - (6, 8): Cosine = 1.000
(6, 8) - (7, 10): Cosine = 0.999
(6, 8) - (7, 6): Cosine = 0.976
(7, 10) - (7, 10): Cosine = 1.000
(7, 10) - (7, 6): Cosine = 0.969
(7, 6) - (7, 6): Cosine = 1.000
Q2: 距離/類似度の解釈#
Q1で扱ったデータ集合において,点\(v=(11, 4)\)との最も類似する点(最近傍点)を求めたい. ユークリッド空間の各次元の意味,最近傍点の定義が下記のような設定である場合,点の類似性を評価する関数としてユークリッド距離,コサイン類似度のどちらを用いるのが適切か考察しながら,最近傍点を求めなさい.
各点は都市の位置情報を表しており,第1次元は「緯度」,第2次元は「経度」を意味する.最近傍点として,物理的距離が近い都市を見つけたいケース.
各点はユーザの購買傾向を表しており,第1次元は「ジャンルAに属する商品を購入した回数」,第2次元は「ジャンルBに属する商品を購入した回数」を意味する.最近傍点として,購買傾向が似ているユーザを見つけたいケース.
# Write your code
for i in range(len(data)):
print(data[i], 'ユークリッド距離 = ', calc_euclidean_dist((11, 4), data[i]))
(2, 2) ユークリッド距離 = 9.219544457292887
(3, 4) ユークリッド距離 = 8.0
(5, 2) ユークリッド距離 = 6.324555320336759
(10, 5) ユークリッド距離 = 1.4142135623730951
(9, 3) ユークリッド距離 = 2.23606797749979
(11, 4) ユークリッド距離 = 0.0
(12, 3) ユークリッド距離 = 1.4142135623730951
(12, 6) ユークリッド距離 = 2.23606797749979
(4, 10) ユークリッド距離 = 9.219544457292887
(4, 8) ユークリッド距離 = 8.06225774829855
(6, 8) ユークリッド距離 = 6.4031242374328485
(7, 10) ユークリッド距離 = 7.211102550927978
(7, 6) ユークリッド距離 = 4.47213595499958
for i in range(len(data)):
print(data[i], 'コサイン類似度 = ', calc_cosine_sim((11, 4), data[i]))
(2, 2) コサイン類似度 = 0.9061831399952652
(3, 4) コサイン類似度 = 0.8372705045624257
(5, 2) コサイン類似度 = 0.9994964752953674
(10, 5) コサイン類似度 = 0.993408935871131
(9, 3) コサイン類似度 = 0.9996349698728535
(11, 4) コサイン類似度 = 1.0
(12, 3) コサイン類似度 = 0.9946184088907779
(12, 6) コサイン類似度 = 0.993408935871131
(4, 10) コサイン類似度 = 0.666330983530245
(4, 8) コサイン類似度 = 0.7259526839058266
(6, 8) コサイン類似度 = 0.8372705045624257
(7, 10) コサイン類似度 = 0.8189029657474978
(7, 6) コサイン類似度 = 0.9359477990383271
Q3: ポケモンデータ再び#
第1章pandas入門のクイズ課題で用いたデータセットpokemonDataを再度ダウンロードし,その内容をpandasデータフレームに変換して変数pokemon_dfに代入しなさい.
その上で,データフレームpokemon_dfから属性HP,Attack,Defense,Sp. Atk,Sp. Def,Speedの値だけを抽出し,データフレームの最初の5件だけを表示しなさい.
# Write your code
pokemon_df = pd.read_table(
'https://raw.githubusercontent.com/lgreski/pokemonData/refs/heads/master/Pokemon.csv', sep=',', na_values=[' '])
target_columns = ['HP', 'Attack', 'Defense', 'Sp. Atk', 'Sp. Def', 'Speed']
pokemon_df[target_columns].head()
| HP | Attack | Defense | Sp. Atk | Sp. Def | Speed | |
|---|---|---|---|---|---|---|
| 0 | 45 | 49 | 49 | 65 | 65 | 45 |
| 1 | 60 | 62 | 63 | 80 | 80 | 60 |
| 2 | 80 | 82 | 83 | 100 | 100 | 80 |
| 3 | 39 | 52 | 43 | 60 | 50 | 65 |
| 4 | 58 | 64 | 58 | 80 | 65 | 80 |
Q4: K-means#
Q3で準備したデータフレームpokenmon_dfとK-meansクラスタリング手法を用いて,第1世代ポケモンを7グループに分けたい.
属性HP,Attack,Defense,Sp. Atk,Sp. Def,Speedのみに注目して,第1世代ポケモンデータにK-meansクラスタリングを適用しなさい.
# Write your code
# クラスタリングを実行
model = KMeans(n_clusters=7, init='random')
model.fit(pokemon_df[pokemon_df.Generation == 1][target_columns])
# 結果を格納
labels = model.labels_
Q5: クラスタの特徴#
Q4で求めた各クラスタに含まれるポケモンデータのHP,Attack,Defense,Sp. Atk,Sp. Def,Speedの平均値を求めなさい.
# Write your code
# クラスタ情報を割り当てる
g1_pokemon_df = pokemon_df[pokemon_df.Generation == 1].assign(
cluster_id = labels
)
# データの集約
g1_pokemon_df.groupby(
'cluster_id' # cluster_idでデータをまとめる
)[target_columns].agg(
'mean' # まとまり毎に平均値を算出
)
| HP | Attack | Defense | Sp. Atk | Sp. Def | Speed | |
|---|---|---|---|---|---|---|
| cluster_id | ||||||
| 0 | 168.333333 | 40.000000 | 23.333333 | 55.000000 | 60.000000 | 38.333333 |
| 1 | 71.666667 | 115.000000 | 117.777778 | 61.111111 | 61.666667 | 63.888889 |
| 2 | 93.592593 | 93.074074 | 84.148148 | 95.444444 | 92.592593 | 72.666667 |
| 3 | 43.150000 | 49.200000 | 43.725000 | 47.050000 | 46.825000 | 62.075000 |
| 4 | 65.045455 | 93.272727 | 65.727273 | 56.545455 | 74.181818 | 93.818182 |
| 5 | 55.103448 | 68.206897 | 82.827586 | 55.344828 | 51.689655 | 39.896552 |
| 6 | 60.190476 | 64.000000 | 62.047619 | 100.714286 | 82.857143 | 98.714286 |
Q6: 階層的クラスタリング結果の比較#
Q1で扱った13個のデータ点について,階層的クラスタリング法を用いて段階的にクラスタに分割したい.
scipy.cluster.hierarchyライブラリのlinkage関数およびdendrogram関数を用いて,Q1で扱ったデータに階層的クラスタリングを適用しなさい.
その際,階層的クラスタリングのクラスタ生成手法として下記3つの方法を用いて,クラスタの生成過程を結果を比較しなさい:
セントロイド法(centroid)
最短距離法(single linkage)
最長距離法(complete linkage)
なお,クラスタ間の距離の尺度にはユークリッド距離を用いること.
# Write your code
# 全ベクトル間の距離を計算.距離の定義にはユークリッド距離を用いる
dist_matrix = distance.pdist(data, metric='euclidean')
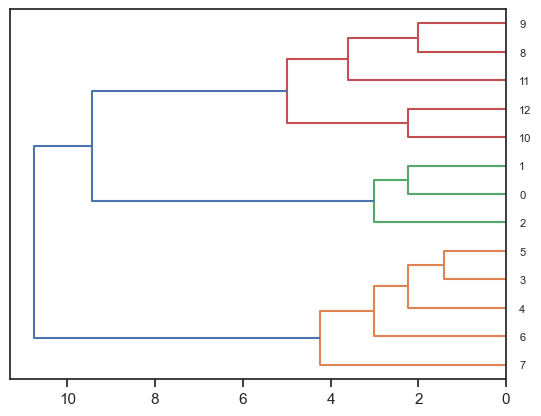
# セントロイド法
centroid_result = linkage(dist_matrix, method="centroid")
# 図の表示
fig = dendrogram(centroid_result, leaf_font_size=8, orientation='left')
plt.show()
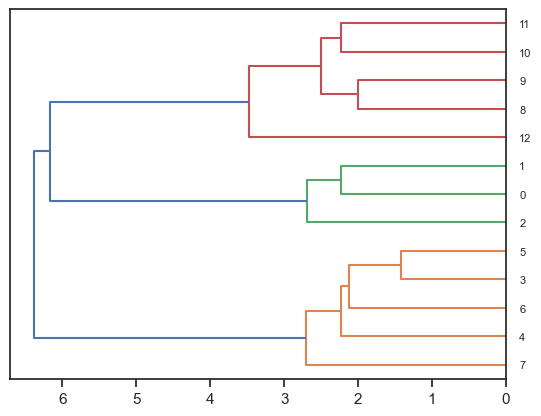
# 最短距離法
single_linkage_result = linkage(dist_matrix, method="single")
# 図の表示
fig = dendrogram(single_linkage_result, leaf_font_size=8, orientation='left')
plt.show()

# 最長距離法
complete_linkage_result = linkage(dist_matrix, method="complete")
# 図の表示
fig = dendrogram(complete_linkage_result, leaf_font_size=8, orientation='left')
plt.show()