4. DBSCAN & クラスタリングの実用上の問題#
このHands-onでは，下記の2種類のデータを用いてDBSCANとクラスタリングの課題を体験する．
人工的なN次元データ
中国は北京市のタクシーの位置データ
Hands-onに先立って，以下のコマンドを実行し，必要なライブラリをインストールしておこう．
# 地図可視化ライブラリのインストール
!pip install folium
必要なライブラリも読み込んでおきます．
# 表形式のデータを操作するためのライブラリ
import pandas as pd
# 行列計算をおこなうためのライブラリ
import numpy as np
# 機械学習用ライブラリsklearnのKmeansクラス
from sklearn.cluster import KMeans
# 機械学習用ライブラリsklearnのDBSCANクラス
from sklearn.cluster import DBSCAN
# 地図の可視化ライブラリ
import folium
# グラフ描画ライブラリ
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
import seaborn as sns;
sns.set(style='ticks')
%matplotlib inline
# ファイルの操作用
import os
# 警告文を表示させないおまじない
import warnings
warnings.filterwarnings('ignore')
4.1. 例題1: 人工データに対するDBSCANクラスタリング#
例題1で用いるデータはUniversity of Eastern Finlandの計算学部が公開している，人工的に作られた8000個の2次元データである．
データの各次元に特に意味はない．
以下のコードを実行して，データをデータフレームに変換しmisc_df変数に代入しよう．
url = "http://cs.joensuu.fi/sipu/datasets/t4.8k.txt"
misc_df = pd.read_table(url, sep="\s+", header=0, names=['x', 'y'])
# 最初の10件のデータを表示
misc_df.head()
| x | y | |
|---|---|---|
| 0 | 68.601997 | 102.491997 |
| 1 | 454.665985 | 264.808990 |
| 2 | 101.283997 | 169.285995 |
| 3 | 372.614990 | 263.140991 |
| 4 | 300.989014 | 46.555000 |
下記コードを実行して散布図を書き，データの分布を確認してみよう．
plt.scatter(misc_df.x, misc_df.y, alpha=0.1)
plt.show()
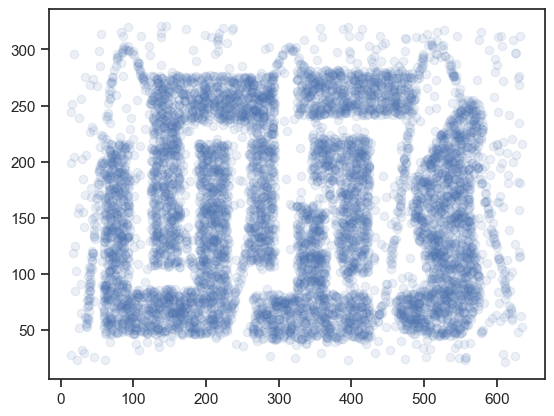
かなり人工的な分布だが，DBSCANの特徴を体験するにはよい題材である． このデータを使って，DBSCANを体験してみよう．
K-meansクラスタリングでは，クラスタリングを行うためにはクラスタ数を指定する必要があった． 一方，DBSCANの特徴として，クラスタ数を指定する必要がないことが挙げられる． DBSCANはどれくらいデータが密集していたら，データの集まりをクラスタを見なすかの閾値さえ与えれば，あとはクラスタ数は自ずと決まる．
まずは上記データに対して，K-meansを適用してみよう．
データを眺めるとクラスタ数は6あるように見えるので，K=6として下記K-meansのコードを実行してみよう．
# クラスタリングを実行（クラスタ数は6）
kmeans_model = KMeans(n_clusters=6, init='random')
kmeans_model.fit(misc_df)
# 結果を格納
kmeans_labels = kmeans_model.labels_
クラスタリングが完了したので，下記コードを実行し，クラスタ毎にデータ点に色づけし可視化してみよう．
plt.scatter(
misc_df.x, misc_df.y,
c=kmeans_labels,
alpha=0.3, # 透明度
s=15, # マーカーのサイズ
cmap="tab20" # カラーパレット（20色対応）
)
<matplotlib.collections.PathCollection at 0x10558a140>
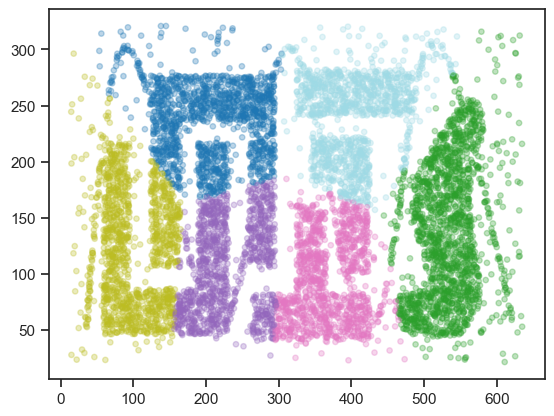
データが6箇所にクラスタリングされたが，期待通りにクラスタリングできていない． 本当は，「コの字」型のクラスタ，「T字」型のクラスタなどが抽出できてほしかったはず．
今回のクラスタリングの結果をよく見ると，K-meansはある点から一定距離内にある範囲をクラスタとして抽出しているように見える（参考: ボロノイ図）． これこそがK-meansの特徴のひとつである． K-meansはクラスタ生成のアルゴリズム上，クラスタの形状が超球状で，クラスタに属するデータ数はクラスタ間で等しいいう仮定を置いている．
おまけにK-meansはクラスタリング時にクラスタ数を指定する必要がある． 今回はたまたまデータの全容を目視することができたため，クラスタ数を予想することができた． しかし，実際はデータは多次元であることが多く，データの全容を視覚的に捉えることは困難である． そのため，クラスタ数を決定するのが難しいこともしばしばある．
上記のデータのように，
クラスタ数を指定せずにクラスタリングしたい
クラスタの形状が超球状以外のものにも対応したい
といったケースで有効な手法がDBSCANである．
早速同じデータにDBSCANを適用してみよう．
機械学習ライブラリscikit-learnにはDBSCANも含まれている．
すでに冒頭でDBSCANクラスを読み込んでいるので，以下のコードを実行すればDBSCANでクラスタリングすることできる．
# クラスタリングを実行
dbscan_model = DBSCAN(eps=10, min_samples=20) #min_samplesはminPtsのこと
dbscan_model.fit(misc_df)
# 結果を格納
dbscan_labels = dbscan_model.labels_
# クラスタリング結果を色づけして可視化
plt.scatter(
misc_df.x,
misc_df.y,
c=dbscan_labels,
alpha=0.3, # 透明度
s=15, # マーカーのサイズ
cmap="tab20" # 濃青はノイズ（-1）ラベル
)
<matplotlib.collections.PathCollection at 0x174e2b8b0>
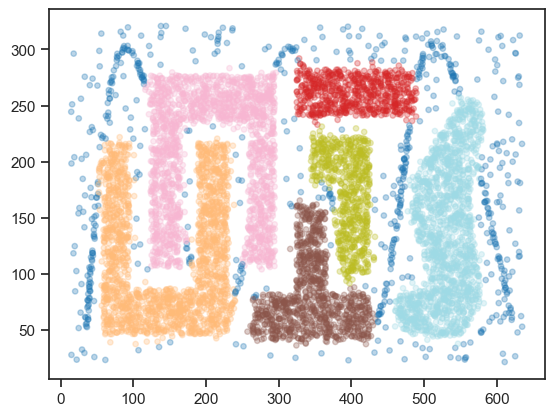
DBSCANによって，「コの字」型のクラスタ，「T字」型のクラスタがうまく抽出できており，直感に合うクラスタリング結果が得られた． またクラスタの周辺にある点が「ノイズ（外れ値）」として識別できていることも確認できる．
上記コードでは，DBSCANのパラメータとして
\(\epsilon\) = 10（eps: クラスタ判定の距離）
\(minPts\) = 20（min_samples: コア点として判定するためのデータ個数）
を設定した．
授業でもお話ししたとおり，DBSCANはパラメータが非常に敏感で，適切な値を設定するのが難しい．
上記コードのeps，min_samplesを適当に変更し，どのように結果が変わるか確認してみよう．
4.2. 例題2: 中国は北京市のタクシーの移動データ#
人工データばかり使っても面白くないので，今度は実データに対してDBSCANを適用してみよう． 次に用いるデータは，Microsoft Researchの研究グループが収集した「北京市におけるタクシーの移動データ」である． このデータは，2008年の2月6日から2月8日にかけて，北京市のタクシー10357台の位置データを一定間隔で収集したもので，全部で1500万レコードのデータが含まれている．
出典は以下の通り:
Jing Yuan, Yu Zheng, Xing Xie, and Guangzhong Sun: “Driving with knowledge from the physical world”. In The 17th ACM SIGKDD international conference on Knowledge Discovery and Data mining, KDD ’11, New York, NY, USA, 2011. ACM.
今回のHands-onで全データを扱うのは時間的に厳しいので，10357台のタクシーのうち，10台のタクシーの2月6日分のデータだけに焦点を当てて分析を行ってみよう．
下記のコードを何も考えずに実行しよう．
データがダウンロードされ，taxi_dfという変数に分析で扱うデータが格納される．
# データをダウンロード
!curl -O https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/06.zip
# zipファイルを解凍
!unzip -q 06.zip -d taxi-dataset
# データをpandasデータフレームに格納
taxi_dfs = []
for i, filename in enumerate(os.listdir("taxi-dataset")):
if i < 10:
_df = pd.read_csv(
'taxi-dataset/{}'.format(filename),
names=['taxi_id', 'timestamp', 'longitude', 'latitude']
).assign(
timestamp = lambda df: pd.to_datetime(df.timestamp)
)
taxi_dfs.append(_df)
else:
break
taxi_df = pd.concat(
taxi_dfs
).drop_duplicates()
# 一時変数とダウンロードしたデータを削除
del taxi_dfs
!rm -rf 06.zip taxi-dataset
# データの表示
taxi_df
| taxi_id | timestamp | longitude | latitude | |
|---|---|---|---|---|
| 0 | 3136 | 2008-02-02 13:38:37 | 116.41042 | 39.94511 |
| 1 | 3136 | 2008-02-02 13:43:37 | 116.41053 | 39.94114 |
| 2 | 3136 | 2008-02-02 13:48:37 | 116.41085 | 39.93205 |
| 3 | 3136 | 2008-02-02 13:53:37 | 116.41151 | 39.91376 |
| 4 | 3136 | 2008-02-02 13:55:56 | 116.41140 | 39.90815 |
| ... | ... | ... | ... | ... |
| 1789 | 7807 | 2008-02-08 17:16:42 | 117.21345 | 40.14508 |
| 1790 | 7807 | 2008-02-08 17:21:42 | 117.21345 | 40.14509 |
| 1791 | 7807 | 2008-02-08 17:26:42 | 117.21346 | 40.14510 |
| 1792 | 7807 | 2008-02-08 17:31:42 | 117.21346 | 40.14510 |
| 1793 | 7807 | 2008-02-08 17:36:42 | 117.21346 | 40.14511 |
16892 rows × 4 columns
ダウンロードしたデータは全部で16892レコードあることが確認できる． また，データは
taxi_id: タクシーのIDtimestamp: データが収集された日時longitude: タクシーの経度latitude: タクシーの緯度
で構成されていることが分かる．
下記コードを実行し，データをX軸を経度，Y軸を緯度とする平面上にマッピングしてみよう．
plt.scatter(taxi_df.longitude, taxi_df.latitude, alpha=0.1, s=5)
plt.show()
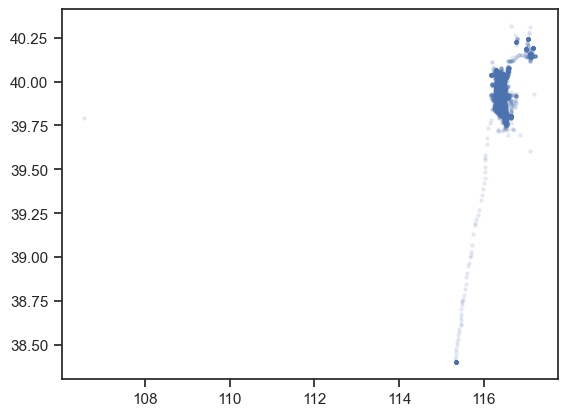
なんだかよく分からない… これを眺めていても面白くないので，下記コードを実行し，データを地図にマッピングしてみよう．
# foliumで地図オブジェクトを作成
beijing_map = folium.Map(location=[39.916668, 116.383331], zoom_start=12)
# 地図上にデータをプロット
for latitude, longitude in taxi_df[['latitude', 'longitude']].values.tolist():
circle = folium.Circle(
radius=30,
location=(latitude, longitude),
fill=True,
fill_opacity=0.2
)
circle.add_to(beijing_map)
# 地図を表示
beijing_map