6. サポートベクターマシン#
このHands-onでは下記2種類のデータを用いて,サポートベクターマシンについて体験する.
手書き数字画像(第5章のHands-onでも用いたデータ)
人工的に作られたある2次元データ
Hands-onに先立って,必要なライブラリを読み込んでおこう.
# 表形式のデータを操作するためのライブラリ
import pandas as pd
# 行列計算をおこなうためのライブラリ
import numpy as np
# データセット
from sklearn import datasets
# K近傍法を実行するためのクラス
from sklearn.neighbors import KNeighborsClassifier
# 決定木を実行するためのクラス
from sklearn.tree import DecisionTreeClassifier
# サポートベクターマシンを実行するためのモジュール
from sklearn import svm
# データ変換のためのクラス
import sklearn.preprocessing as preprocessing
# 交差検証を行うためのクラス
from sklearn.model_selection import StratifiedKFold
from sklearn.model_selection import cross_validate
# 評価指標(マクロ精度)
from sklearn.metrics import balanced_accuracy_score
from sklearn.metrics import accuracy_score, precision_score
# グラフ描画ライブラリ
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
6.1. 例題1: MNIST手書き数字データ#
例題1では,K近傍法のHands-onで用いたMNISTデータセットを用いて,手書き数字の識別するサポートベクターマシン分類器を構築しよう. データセットの詳細は前回のHands-onを参照のこと.
それでは,以下のコードを実行してMNISTデータセットを読み込もう.
mnist_dataset = datasets.load_digits()
X_mnist = mnist_dataset.data
y_mnist = mnist_dataset.target
前回の「K近傍法」の授業では,機械学習を実際に行う際には
前処理
学習・評価の流れ
評価手法
に関するお作法があることを学んだ. K近傍法や機械学習のお作法の復習のために,まずはK近傍法を使ってMNISTの分類器の構築・評価を行ってみよう. 今回は5分割交差検証を行い,評価手法にはマクロ精度(Balanced Accuracy)を用いることにする.
下記コードは,MNISTデータセットにK近傍法を適用する例である.
# 5分割「層別化」交差検証の準備(乱数を固定)
k_fold = StratifiedKFold(n_splits=5, shuffle=True, random_state=12345)
# 評価指標(マクロ精度)
score_funcs = ['balanced_accuracy']
# K近傍法のモデルの定義(K=5で設定)
K = 5
knn_model = KNeighborsClassifier(n_neighbors=K, metric="euclidean")
# 交差検証をしながら分類器を構築・評価
results = cross_validate(knn_model, X_mnist, y_mnist, cv=k_fold, scoring=score_funcs)
# 交差検証の評価スコアを平均としてまとめる
print("Balanced accuracy: ", np.mean(results['test_balanced_accuracy']))
Balanced accuracy: 0.9870943800943801
マクロ精度は98.7%程度になった. K近傍法でも十分な分類性能を発揮することが分かる.
次はサポートベクターマシンで手書き数字画像の分類器を構築・評価してみよう.
機械学習万能ライブラリであるsklearnは,サポートベクターマシンに関するクラスも提供している.
sklearnではサポートベクターマシンに関連するクラスとして
分類問題を扱うための
svm.SVCクラス回帰問題を扱うための
svm.SVRクラス
の2種類を提供している.
今回は分類問題を扱うので,svm.SVCクラスを用いる.
今回はカーネルトリックは使わず,単純な線形サポートベクターマシンを使ってみよう.
sklearnライブラリを使えば,上のK近傍法コードをたった一行変えるだけで,サポートベクターマシンによる分類器の構築・評価ができてしまう.
以下,修正したコードを実行してみよう.
k_fold = StratifiedKFold(n_splits=5, shuffle=True, random_state=12345)
score_funcs = ['balanced_accuracy']
# 線形サポートベクターマシン(ここが修正点)
svm_model = svm.SVC(kernel='linear')
results = cross_validate(svm_model, X_mnist, y_mnist, cv=k_fold, scoring=score_funcs)
print("Balanced accuracy: ", np.mean(results['test_balanced_accuracy']))
Balanced accuracy: 0.9787107780048956
サポートベクターマシンを用いたときのマクロ精度は98%程度になった. MNISTデータセットの分類問題に関しては,サポートベクターマシンとK近傍法の性能は同程度のようだ.
6.2. 例題2: 線形分離不可能なデータに対するサポートベクターマシン#
次の例題では,人工的な2次元データの分類問題を扱う. まずは以下のコードを実行して,今回の例題で用いるデータを読み込もう.
from sklearn.datasets import make_circles, make_moons
moons = make_circles(n_samples=300, noise=0.1, factor=0.6, random_state=777)
X_moon = moons[0]
y_moon = moons[1]
ax = sns.scatterplot(x=X_moon[:, 0], y=X_moon[:, 1], hue=y_moon)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
plt.show()
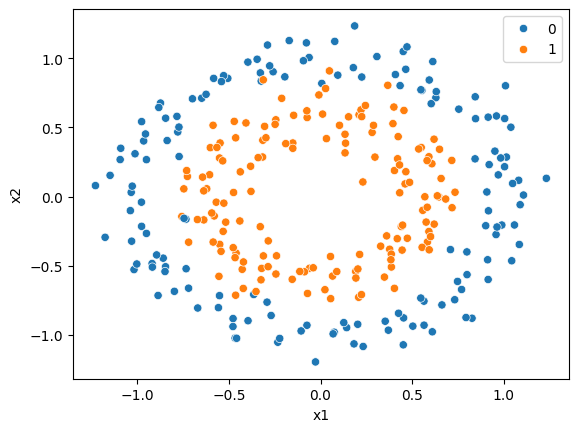
今回用いるデータは,授業でも扱った「ドーナツ型」のデータ分布をしている. 内側にオレンジ色の点(ラベル1)が,外側に青色の点(ラベル0)が分布している. これらデータを用いて,データがラベル1かラベル0かを分類する分類器を構築してみよう.
まず,線形SVMを用いて分類器を構築・評価してみよう. 以下のように例題1のコードをほぼそのまま流用することで,線形SVMの学習・評価ができる.
k_fold = StratifiedKFold(n_splits=5, shuffle=True, random_state=12345)
# 今回は評価指標として適合率(precision)と再現率(recall)を使用
score_funcs = ['precision_macro', 'recall_macro']
# 線形サポートベクターマシン(ここが修正点)
svm_model = svm.SVC(kernel='linear')
results = cross_validate(svm_model, X_moon, y_moon, cv=k_fold, scoring=score_funcs)
print("Precision: ", np.mean(results['test_precision_macro']))
print("Recall: ", np.mean(results['test_recall_macro']))
Precision: 0.4916286178314683
Recall: 0.49333333333333335
適合率も再現率も49%なので,デタラメにラベルを答える場合とほぼ性能が分からないと言える. 授業でも説明したが,素のサポートベクターマシン(線形SVM)は,今回用いるデータセットのような線形分離不可能な分類問題にはうまく対応できない. このような場合は,データを高次元に写像することでうまく対応できる可能性がある.
普通の流れならここでカーネルトリックを用いた非線形SVMを用いるのだが,少し寄り道をしよう. 手動でデータを高次元に写像し,そのデータに対して線形SVMを適用してみよう.
今回用いたデータは2次元データであった. ここで,1次元目の要素を\(x_1\),2次元目の要素を\(x_2\)としたとき,3次元目の要素として\(\sqrt{x_1^2+x_2^2}\)をデータに追加しよう. 以下はそのためのコードである.
X_moon_new = np.insert(X_moon, 2, np.sqrt(X_moon[:, 0]**2+X_moon[:, 1]**2), axis=1)
# データの末尾10件のみ表示
X_moon_new[-10:, :]
array([[ 0.22518032, 0.8642077 , 0.89306278],
[ 0.96372889, -0.22060904, 0.98865653],
[ 0.38431474, -0.4575082 , 0.59750445],
[ 0.23280386, -1.08479306, 1.10949251],
[ 0.54765035, -0.73467811, 0.91633664],
[ 0.48637921, 0.10255874, 0.49707447],
[-1.02809832, 0.07486352, 1.0308204 ],
[-0.84914995, -0.54263203, 1.00772276],
[-0.69927825, 0.70696368, 0.99437805],
[-0.4580985 , -1.02554963, 1.12321248]])
3次元目の要素がデータに追加された.
新たに作ったX_newを使って,再度サポートベクターマシンを適用してみよう.
以下,そのコード例である.
k_fold = StratifiedKFold(n_splits=5, shuffle=True, random_state=12345)
score_funcs = ['precision_macro', 'recall_macro']
svm_model = svm.SVC(kernel='linear')
# XをX_newに修正
results = cross_validate(svm_model, X_moon_new, y_moon, cv=k_fold, scoring=score_funcs)
print("Precision: ", np.mean(results['test_precision_macro']))
print("Recall: ", np.mean(results['test_recall_macro']))
Precision: 0.9636484983314795
Recall: 0.9633333333333335
適合率も再現率も大幅に向上した. 今回のデータは円の形に分布していたので,3時限目のデータとして円の半径に相当するような要素を追加した. それが功を奏して分類器の性能が向上した.
しかし,このような都合の良いの高次元写像をデータに応じて地力で見つけるのは容易ではない. こんなときに有用なのがカーネルトリックを用いた非線形SVMである. 例題の締めとして,RBFカーネルを用いた非線形SVMによる分類器の構築・評価を行ってみよう.
sklearnライブラリを用いれば,非線形SVMも簡単に実行できてしまう.
今回はパラメータチューニングはせず,デフォルトの状態でRBFカーネルを用いてみよう.
以下のコードを実行して,(手動で高次元化していない)元のデータを用いた学習・評価を行ってみよう.
k_fold = StratifiedKFold(n_splits=5, shuffle=True, random_state=12345)
score_funcs = ['precision_macro', 'recall_macro']
# カーネルにRBFカーネルを指定
svm_model = svm.SVC(kernel='rbf')
# 交差検証
results = cross_validate(svm_model, X_moon, y_moon, cv=k_fold, scoring=score_funcs)
print("Precision: ", np.mean(results['test_precision_macro']))
print("Recall: ", np.mean(results['test_recall_macro']))
Precision: 0.9638575268817204
Recall: 0.9633333333333335
データを手動で高次元空間に写像しなくても,RBFカーネルが良い具合に振る舞ってくれた.
6.3. クイズ#
※ 以下のクイズの回答にGoogle Colaboratoryを使いたい方はコチラをクリック.
6.3.1. Q1: 実行時間の計測#
機械学習モデルの交差検証を簡単に行ってくれるsklearnライブラリのcross_validate関数は,その返値(辞書)には
学習の所要時間(
fit_time)評価(推論)の所要時間(
score_time)
に関する情報が格納されている(参考).
この情報を用いて,例題1におけるMNIST分類器を
多項式カーネル(
kernel='poly')を用いたサポートベクターマシンK近傍法(
K=5)決定木
の3つの機械学習手法で構築した際の
分類器の性能
分類器の構築(学習)にかかる時間
分類器の評価(推論)にかかる時間
について比較を行いなさい.
6.3.2. Q2: 年収カテゴリ分類の性能比較#
Q1で行った同様の比較を,第5章のクイズで取り組んだ年収カテゴリ分類問題に対して行いなさい.
